Die Weierstraß-Funktion

Ich habe mich heute an mein Proseminar in Analysis erinnert.  Ein Thema war eine überall stetige, aber niergendwo diffenzierbare Funktion.  Das es eine solche Funktion gibt war lange Zeit unbekannt.

Aus der Diffenzierbarkeit folgt die Stetigkeit. Diese Umkehrung dieser Aussage gibt nicht. Ein Beipiel ist die Betragsfunktion. Diese ist im Nullpunkt nicht diffenzierbar. Der Mathematiker Karl Weierstraß hat im 19. Jahrhundert eine Funktion konstruiert, welche überall stetig, aber an keiner Stelle differenziebar ist.

Das ist nicht die Orginale Funktion von ihm, welche er zuerst vorgestellt hat. Diese Funktion sieht aber aus wie eine Sinuskurve. Die Zacken im Plot entstehen, weil die Summe nicht bis Unendlich läuft. Aus Gründen der Zahlendarstellung im Rechner, habe ich die Summe nur bis 50 laufen lassen.

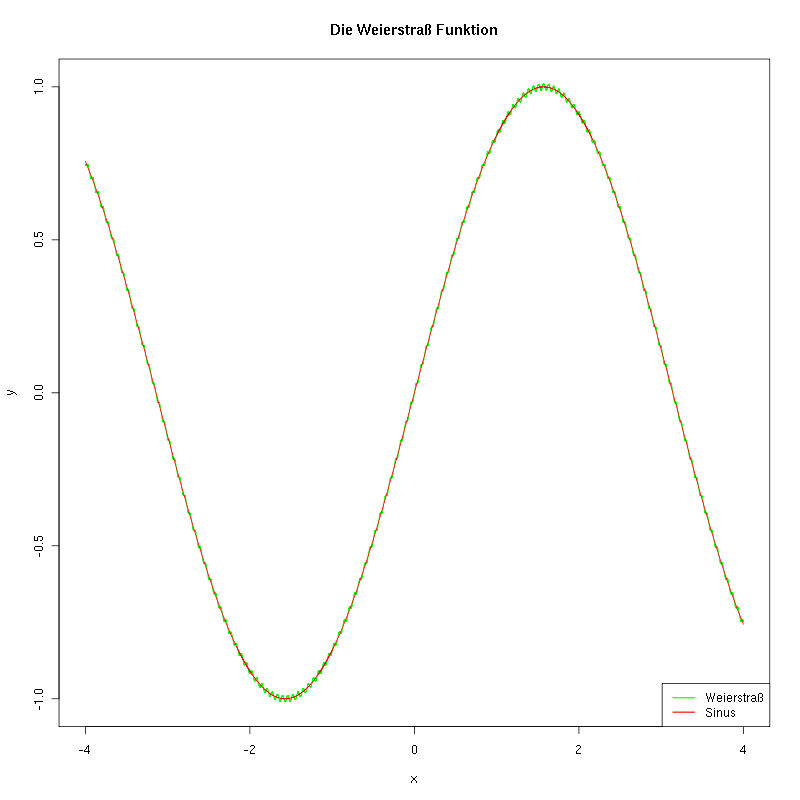
Seine erste Funktion sah wie folgt aus:

Unter den folgenden Bedingungen: